Zadanie 8. Dane są ułamki
35/
396 oraz
28/
297. Znajdź najmniejszą ze wszystkich liczb, przy dzieleniu której przez każdy z danych ułamków otrzymuje się liczby całkowite.
Odpowiedź:
140/
99.
Zadanie 7. W kole o środku w punkcie
O poprowadzono cięciwę, która nie jest średnicą. Punkt
A dzieli tę cięciwę na dwa odcinki o długościach 5 cm i 11 cm. Oblicz obwód i pole tego koła, jeżeli odcinek OA ma długość 5 cm.
Odpowiedź: P =
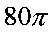
cm
2; Ob =
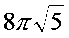
cm
Zadanie 6. W trapezie równoramiennym boki równoległe AB=52 cm, CD=20 cm. Przekątna trapezu tworzy z ramieniem kąt prosty. Oblicz wysokość i pole tego trapezu.
Odpowiedź: Wysokość ma długość 24 cm, pole 864 cm
2.
Zadanie 5. Koło o średnicy a na odcinku 12 m wykona 8 obrotów, a koło o średnicy b na tym samym odcinku wykona 10 obrotów. Suma pól tych kół jest równa
369/
400π. Oblicz pole każdego koła.
Odpowiedź: Pole mniejszego koła jest równe
9/
25π, a większego
9/
16π.
Zadanie 4. Uczeń odpowiedział poprawnie na 14 pytań testu, co stanowi 70% wszystkich pytań. Ile pytań testu pozostało bez prawidłowej odpowiedzi?
Odpowiedź: 6 pytań.
Zadanie 3. Franek miał dwa naczynia w kształcie sześcianu; jedno o krawędzi 4dm, a drugie o krawędzi 5dm. Do mniejszego sześcianu nalał wody do pełna, a następnie przelał ją do większego sześcianu. Jaka będzie wysokość wody w dużym sześcianie wyrażona w milimetrach?
Odpowiedź: 256 mm
Zadanie 2. Krysia ma a lat, a jej siostra Zosia jest od niej o 5 lat starsza. Zapisz wyrażenie przedstawiające, ile lat łącznie będą miały siostry za 12 lat.
Odpowiedź: 2a + 29
Zadanie 1. W ciągu trzech dni Zosia zebrała średnio 16 znaczków. Czwartego dnia zdobyła 20 znaczków, powiększając swoją średnią. Ile wyniosła ta średnia po czterech dniach?
Odpowiedź: 17